The Steepest-Descent Method - ppt download
Por um escritor misterioso
Descrição
Steepest-Descent Method Complex Integral: The method was published by Peter Debye in Debye noted in his work that the method was developed in a unpublished note by Bernhard Riemann (1863). Peter Joseph William Debye (March 24, 1884 – November 2, 1966) was a Dutch physicist and physical chemist, and Nobel laureate in Chemistry. Georg Friedrich Bernhard Riemann (September 17, 1826 – July 20, 1866) was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity.
Hence we have: as. Note: In a similar manner, we could obtain higher-order terms in the asymptotic expansion of the Bessel function or the Gamma function.
Hence we have: as. Note: In a similar manner, we could obtain higher-order terms in the asymptotic expansion of the Bessel function or the Gamma function.

Riemannian proximal gradient methods

Multiomics Analysis Provides Novel Pathways Related to Progression of Heart Failure

METHOD OF STEEPEST DESCENT - ppt download

The Steepest-Descent Method - ppt video online download

Distinguishing Progression from Pseudoprogression in Glioblastoma Using 18F-Fluciclovine PET

Steepest descent method
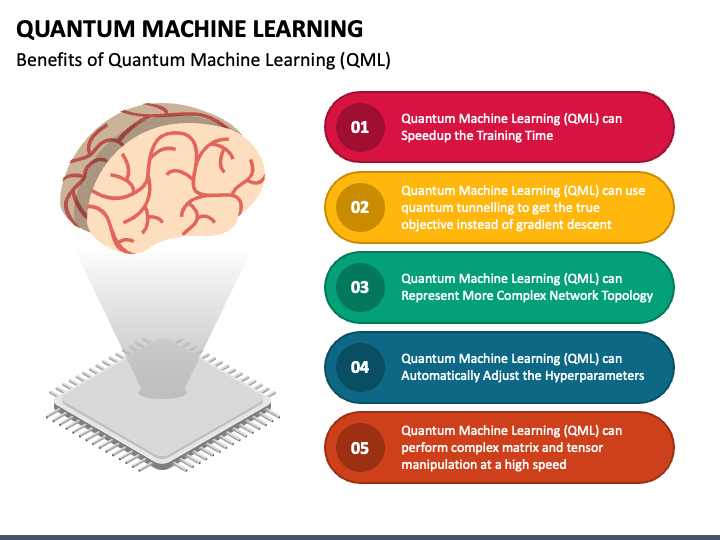
Quantum Machine Learning PowerPoint Template - PPT Slides
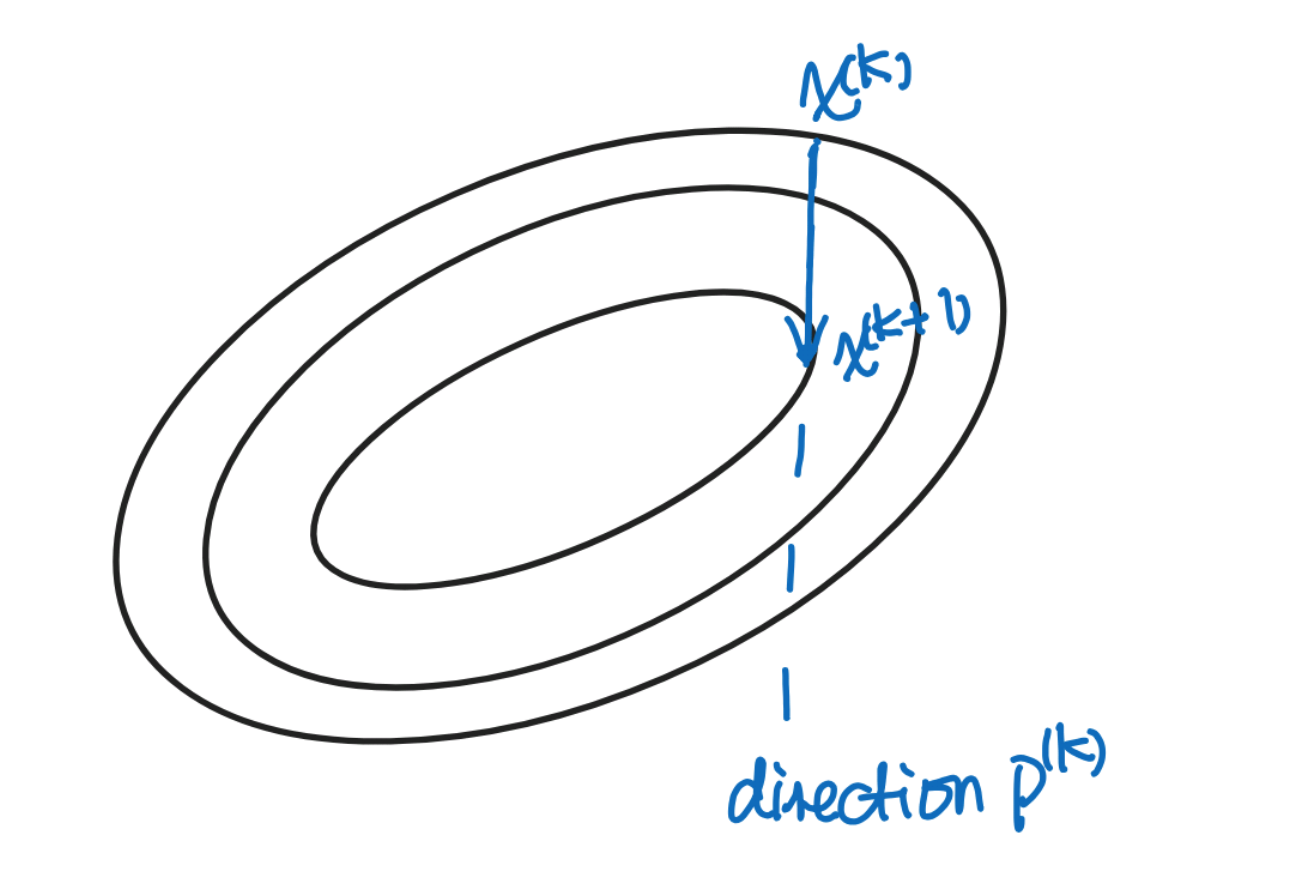
Descent method — Steepest descent and conjugate gradient, by Sophia Yang, Ph.D.

SOLUTION: Steepest descent method ppt - Studypool

Gradient descent method

Differentially Private Deep Learning with Iterative Gradient Descent Optimization

Christian S. Perone on X: I spent many long nights preparing this material for a visual introduction to optimization in Deep Learning, ranging from 1st-order methods, 2nd-order and Natural Gradient (and approximations

PPT – Chapter 6: DerivativeBased Optimization PowerPoint presentation
de
por adulto (o preço varia de acordo com o tamanho do grupo)


.png)




